Data Structures & Algorithms
Hash Tables
Guide: How to implement a hash table (in C) (benhoyt.com)
- Create Array of certain size (generally any power of 2)
- Generate Hash from key
hash(key) & (len(array)-1)-> storage position- Modulo would be the general case, but since size is 2n we can use binary-AND which is much faster
- Probe position. If already occupied (collision):
- Open addressing, linear probing: Add 1 to index and try again (until empty slot found)
- Separate chaining: Store values as linked list of results
- Other methods: Hash table - Wikipedia
- Store value as well as hash in the resulting position
- Hash is needed to resolve collisions
- Some tables put the data separately in a flat array and only store hash+index, this saves space for large data structs
- Lookup is constant (O(1) amortized) as
index = hash(key) & (len(array)-1)+ collision resolution
- Certain details of the general approach listed above can vary in practice (e.g. some tables have other probing strategies)
- Entries of the hash table are usually called "slots". Some tables allocate multiple slots at once in "buckets" (usually the size of a cache line). Sometimes the words are used interchangeably.
- "Tombstones" are special values often used with open addressing to mark deleted slots (since you cannot mark them as empty, which would break probing chains). They are re-used on insertion and should count towards the load factor.
- For open addressing hash table may never be too full. Usually load factors between 0.5 and 0.9 are used, based on the tables collision resolution technique (0.75 or 0.9 seem common). Else storing and lookups can become really slow (infinite loop when table is 100% full)
- The linked list approach requires extra memory allocations during store and handling a linked list is slower in general (not cache friendly)
- High performance tables use SIMD for probing by storing a small part of the hash in a separate array, skipping to a "general region" of that array with most of the hash bits and then checking multiple slots with SIMD + the remainder of the hash
- Benchmark: An Extensive Benchmark of C and C++ Hash Tables | A comparative, extendible benchmarking suite for C and C++ hash-table libraries.
- Implementation with detailed explanation: Hash Tables · Crafting Interpreters
Linked List vs Array
C++ benchmark - std::vector VS std::list | Blog blog("Baptiste Wicht"); (baptiste-wicht.com)
https://www.rfleury.com/p/in-defense-of-linked-lists
Sorting
Vergleich mit Animation: Sorting Algorithms Animations | Toptal®
Insertion Sort
Einer der besten Algorithmen, wenn Liste bereits fast sortiert ist. Ebenfalls gut, wenn Datenmenge klein ist. Wird daher oft in anderen Algorithmen verwendet, wenn Liste in kleinere Stücke geteilt wurde.
Sehr langsam wenn Liste invertiert ist.
i ← 1
while i < length(A)
x ← A[i]
j ← i
while j > 0 and A[j-1] > x
A[j] ← A[j-1]
j ← j - 1
end while
A[j] ← x
i ← i + 1
end while
Quicksort
Gut bei großen Datenmengen.
Sehr gut wenn Liste invertiert ist.
Nicht so gut wenn Liste bereits fast sortiert ist.
Grundsätzlich für die meisten Anwendungen gut geeignet.
"in memory" sort, braucht keinen zusätzlichen Speicher (außer eine handvoll temporäre Variablen für Wertetausch, Pivot, Iteratoren).
// Sorts a (portion of an) array, divides it into partitions, then sorts those
algorithm quicksort(A, lo, hi) is
if lo >= 0 && hi >= 0 && lo < hi then
p := partition(A, lo, hi)
quicksort(A, lo, p) // Note: the pivot is now included
quicksort(A, p + 1, hi)
// Divides array into two partitions
algorithm partition(A, lo, hi) is
// Pivot value
pivot := A[lo] // Choose the first element as the pivot
// Left index
i := lo - 1
// Right index
j := hi + 1
loop forever
// Move the left index to the right at least once and while the element at
// the left index is less than the pivot
do i := i + 1 while A[i] < pivot
// Move the right index to the left at least once and while the element at
// the right index is greater than the pivot
do j := j - 1 while A[j] > pivot
// If the indices crossed, return
if i >= j then return j
// Swap the elements at the left and right indices
swap A[i] with A[j]
In C:
void qsort( void* ptr, size_t count, size_t size,
int (*comp)(const void*, const void*) );
// ptr - start of array
// count elements of size bytes each
// comp - comparison function (returns -1 if first arg is < second arg, 1 if > and 0 if equal)
// Is not guaranteed to use quicksort, some implementations use insertion sort for small arrays or merge sort
stl::sort vs qsort: C qsort() vs C++ sort() - GeeksforGeeks, Beating Up on Qsort | Performance Matters
- stl::sort is faster because the compiler can inline the comparison code generated by the templates
- qsort on the other hand relies on indirect function pointers, which are opaque for compilers
- qsort can be made faster by copying implementation and inlining comparator
Radix Sort
Super fast, but only for integers: Beating Up on Qsort | Performance Matters
Directly sorts numbers into their final buckets by comparing them "digit by digit" basically (usually base-256 is used instead of base-10).
Needs additional memory for the buckets (which can slow it down, if not properly optimized).
Time complexity is O(n) instead of O(n*log(n)) for most other sorting algorithms.
Also needs special attention if negative numbers are involved (additional sort on the sign bit).
Quadtrees and Grids
Great set of posts:
data structures - Efficient (and well explained) implementation of a Quadtree for 2D collision detection - Stack Overflow
performance - What is a coarse and fine grid search? - Stack Overflow
Multi-stage Tables
Two-stage tables for storing Unicode character properties - strchr.com
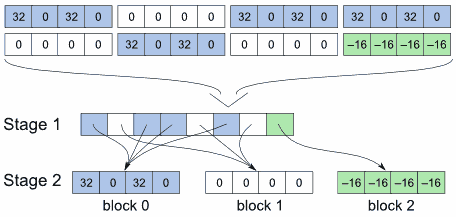
- A form of compression
- Take an array of data and split it into blocks/chunks of equal size (e.g. 256 bytes)
- Now go through the blocks and every time you encounter a new unique byte sequence, add it to a list (the second stage table) and keep a reference to it in an array (the first stage table)
- When looking for a specific byte, go to its position in the stage 1 table (which is the byte offset divided by the block size truncated down), follow the reference and then go to the byte offset in that block
unsigned get_property(unsigned ch)
{
const unsigned BLOCK_SIZE = 256;
unsigned block_offset = stage1[ch / BLOCK_SIZE] * BLOCK_SIZE;
return stage2[block_offset + ch % BLOCK_SIZE];
}
- This essentially compresses the array down to the sum of all unique blocks plus overhead for the stage 1 table (which is number of blocks times sizeof reference type)
- The less unique byte sequences there are, the higher the compression ratio
- It's ideal for data with a lot of empty space or repeating patterns (in this example a lookup table for unicode character properties)
- Somewhat similar to Dictionary coder - Wikipedia used in LZMA (zip)
Branchless Programming
https://en.algorithmica.org/hpc/pipelining/branchless/ (generally a good resource for in-depth low-level programming tips)
Branchy:
for (int i=0; i < len; i++)
if (a[i] < 50)
sum += a[i];
Branchless:
for (int i=0; i < len; i++)
{
sum += (a[i] < 50) * a[i];
// alternative (is also translated to cmov):
sum += (a[i] < 50) ? a[i] : 0;
}
First code compiles with cmp and jne (jump) assembly instructions, second uses cmov (conditional move). This can be still faster especially when the branch cannot be reliably predicted (e.g. the if condition returns true or false randomly/50% of the time each). It is essential for usage of SIMD, since that does not have branches.
Branchless code like this will be slower when code in the branches is compute-intense, since essentially both branches are always computed.
Using predication eliminates a control hazard but introduces a data hazard. There is still a pipeline stall, but it is a cheaper one: you only need to wait for
cmovto be resolved and not flush the entire pipeline in case of a mispredict.
Many code snippets can be converted to be branchless. Simple code like the one above usually is converted by the compiler automatically when optimizations are turned on.